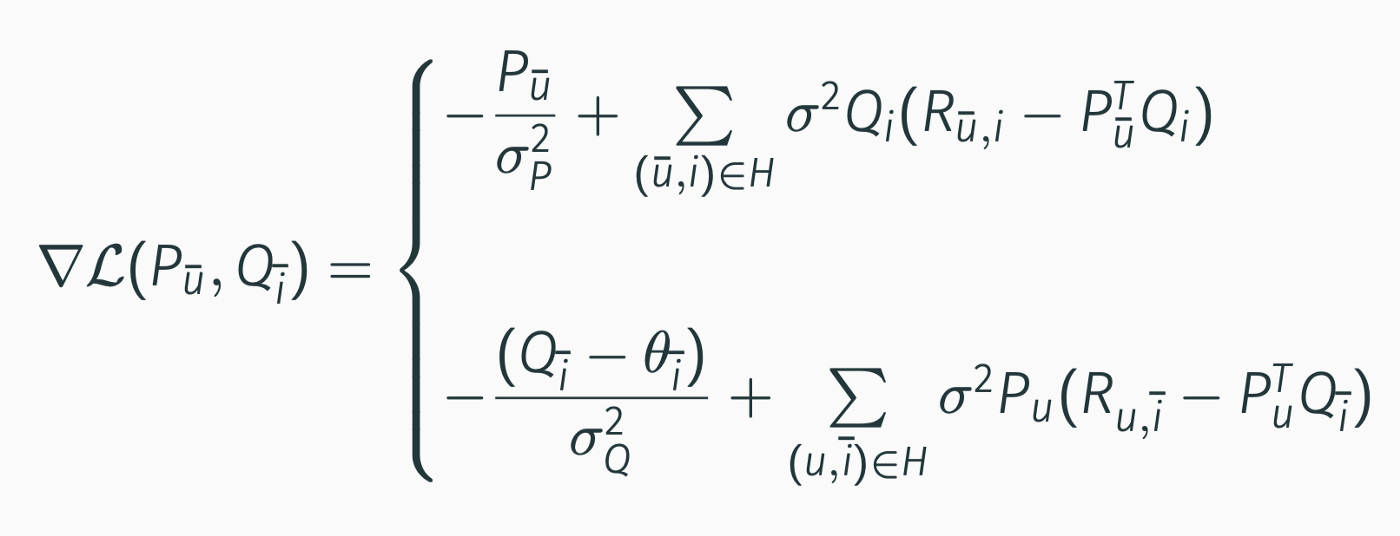Collaborative Topic Modeling
Created: 2022-05-03 10:41
#paper
Main idea
Collaborative Topic Modeling (CTM) is a recommender system for text-based items buildt upon Probabilistic Matrix Factorization (PMF) and LDA.
CTM is superior compared to PMF approach because it is able to do out-of-matrix predictions, i.e. it can derive latent vector of qualities for unrated items.
In deep
A latent qualities vector for a document i, $Q_i$ is represented as: $Q_i=\theta_i+\epsilon_i$, where $\theta_i$ is the (Kx1) vector of topic proportions for item i obtained from traditional LDA estimates, and $\epsilon_i$ is a (Kx1) offset vector that adjust topic proportions by considering ratings.
The generative process for CTm is shown in the following image:
Where $\sigma^2_P$ and $\sigma^2_Q$ represent the variance we impose a priori on the distribution of the elements of the vectors in P and Q. Similarly, $\sigma^2_u$ represents the variance we impose a priori on the distribution of the ratings. $Dir(\alpha)$ is the Dirichlet distribution.
So we are interested into learning the paramenters $\theta_i$, $Q_i$ and $P_u$. We can do this using Maximum Likelihood, where the likelihood od our data is defined as: $p(P,Q,\theta, R|\sigma_P,\sigma_Q,\sigma, \beta,\alpha)=p(P|\sigma^2_P)p(Q|\theta,\sigma^2_Q)p(\theta,w|\alpha,\beta)p(R|P,Q,\sigma^2)$
As often happen, it is more convenient to work with the log-likelihood.
By working on each component independently:
First Component:
Second Component:
Third Component:
That, after imposing $\alpha=1$ for convenience, becomes:
Fourth Component:
Then, by riassemblying everything:
To estimate the parameters, we obtaine $\theta$ using standard LDA and then optimize for [P, Q] via gradient ascent (originally in the paper they used Coordinate Ascent method for optimization, but this is computationally heavier).
The gradient of the log-likelihood with respect to [P,Q] is:
