Gradient Descent
Created: 2022-12-02 14:50
#note
Gradient descent is an optimization algorithm used to find the values of parameters of a function to minimizes a cost function.
It is an iterative approach, in which at each iteration we compute the derivative of the cost so that we know the direction towards which we can get a lower cost at the next iteration. The coefficient values are then updated, often with the use of a learning rate.
In the last scenario described, the cost is calculated over the entire training dataset for each iteration. One iteration is called batch, so this approach is also called batch gradient descent.
Another way of using gradient descent consists in running a training epoch for each example. This approach is easier to store in memory, since we do not have to have all the sample in memory at once, but we need much more updates and also the training is much more unstable. On the other hand, bigger updates can help to escape from local minima. This is called Stochastic gradient descent.
There is a third option, Mini-batch gradient descent, which combines the other two concepts. It splits the dataset into small batches (32, 64, 128...) and performs updates on each of those batches.
Problems with gradient descent:
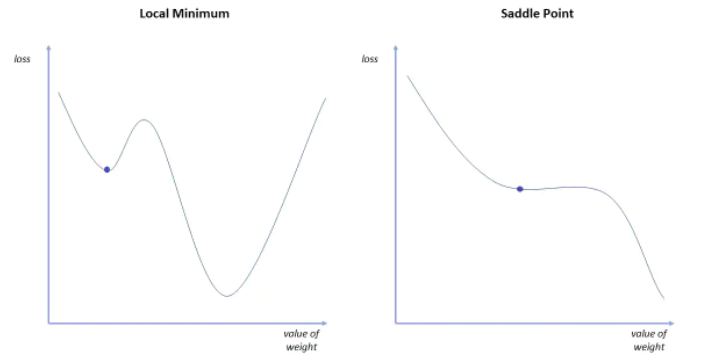
- local minima, when dealing with non-convex problems;
- saddle points, in which the negative gradient exists only on one side of the point;
- Vanishing/Exploding gradients, they happen when the gradient is too small/big and the updates are too small/big
References
Tags
#ml